Recursion

( Tower of Hanoi would be solved in the next article.)

Hello Guys, I'm Glad to tell you that this is my first blog. I can't thank Kunal Kushwaha Bhaiya enough to dedicate his life to creating awareness in the soft-tech industries and coding community. Recommending his YouTube Channel is the best thing Google ever did for me.

I've crossed out all useless things off my chart and hope to stay online in the community as much as possible. Please give your feedback on my blog , coding etc..... I'm all for improving myself, therefore criticism is welcome.

Tower of Hanoi is a puzzle game for kids. It's fun, challenging and colorful and no, it's not Rubik's Cube or anything like that. There are three ( could be more ) poles and concentric rings of different diameters arranged as shown in the figure.

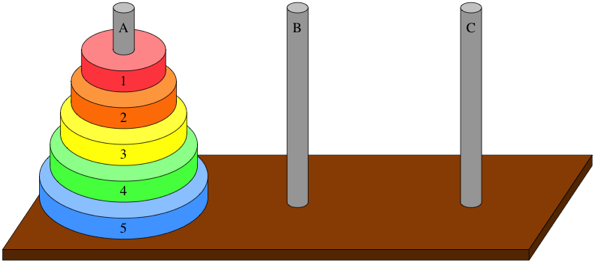
The goal is to move all the rings from pole A to pole B. Rings must be moved only one at a time and make sure you don't place a larger ring ( or ring with a larger number ) over a smaller one.

Before glancing at the next picture, I strongly suggest you ponder on the possible solution to this problem. But before we code it, let's understand what is a recursive function and why is it not just a bit tricky to understand at first but also mind-blowing to finally get it.

What are functions?

We know that a function is a piece of code or instruction that can be called whenever required without repeating the code. The main syntax consists of a functionName, Parameters or Arguments, and Code Body. It may or may not consist of a Return statement. Also if the language being used isn't dynamically typed(i.e memory being allocated during runtime) you have to specify the data type of Return value. So whenever you want to execute a certain set of codes or perform an action on certain variables, you can Call the function .

For example:

# Defining a function to print the table of the input number .
def printTable(x):
     for i in range(1,11):
    # Displaying the table , multiples 1 to 10
        print('{} X {} =  {}'.format(x,i,x*i))
     # my function definition is complete and notice that it has no return statement

# asking user for input 
no=int(input(' Enter a number to Print Table:  '))
#calling the function printTable()
#Displaying the table
printTable(no)

Recursive Functions

I'm not going deep into the basics. For this article let's talk about Recursive Functions.

Here is an example of Recursive Functions to find the factorial ( n!=1x2x3x4x.....n) of a number.

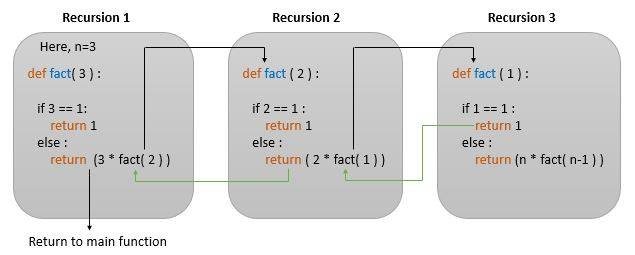
The factorial is n ( here, 3 ) is essentially figured out like this:

3!= 3 x 2!

2!= 2 x 1!

1!=1

def re(x):

    if x==1:
        return 1
    else :
        return x*re(x-1)

x=int(input("enter a no "))

print( ' Factorial of %d is %d' %(x , re(x)))

Let's say you entered 5 as input. Since 5 != 0 isn't true, else part would be executed and the function returns 5*re(4), let's call this firsthand output FS.i.e FS=5*re(4).

When re(4) is executed in the memory, the else part would be executed again and this time the function would return 4*re(3).At this moment, FS=5*4*re(3).

When re(3) is executed in the memory, the same thing would happen and FS would be stored as FS=5*4*3*re(2). Once again, the same thing would repeat and we would have FS=5*4*3*2*re(1). We have already defined the case, especially for 1 and finally when the iteration is over the original or the starting re() function would return 5*4*3*2*1, our desired factorial.

Three things ought to be kept in mind while constructing our Recursive Functions ......

1.> Define the base case first. Here, our base case was to assign re(1)=1. Base case is necessary because it signals the execution chain to stop calling functions.

2.>Figure out, if and how the problem can be broken down into simpler parts. We can solve only those problems using recursion which can be broken down into smaller parts and every part resembles the original problem.

3.>Find the Recurrence Formula or the Recurrence Relation. As the name suggests, it's the relationship between the terms of a Recursive function's, in terms of a formula.

// Here , the Recurrence Formula is : 
// re(x) = x * re (x-1) , i.e x! = x * { (x-1)! }

That's all for today friends, let me know what improvements could be made anywhere in the entirety of the article. In the next articles, we will go deeper into Recursive Functions and in the end, we will see the solution to Tower of Hanoi problem. My wish was to let people who are new to Recursion, a new problem to ponder upon it and trust me, solving this problem using recursion is a beautiful experience. I hope you enjoyed reading.

Thank You.

Recursion and Tower of Hanoi Problem

( Tower of Hanoi would be solved in the next article.)

What are functions?

Recursive Functions